고정 헤더 영역
상세 컨텐츠
본문
백준에서 DP문제를 발견한김에 정리해보려고 한다

동적 계획법 이라고도 불리는 DP(Dynamic Programing)는
큰문제를 작은문제들로 나누어 해결하는 분할정복(Divide and Conquer)과 유사하지만
작은문제의 해가 큰 문제를 해결할때 사용된다는점에서 차이가 있다(중복계산을 피할수 있음).
문제: 1463번: 1로 만들기
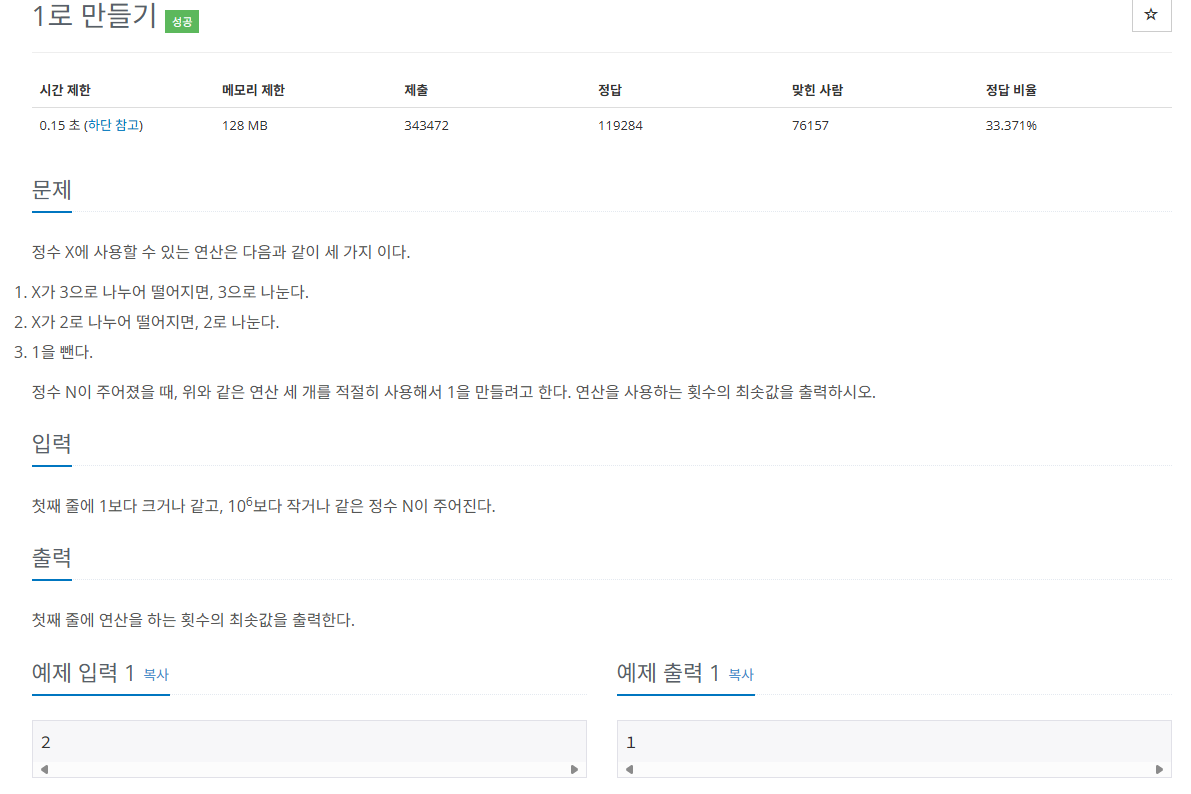
풀이(파이썬)
import sys
N = int(sys.stdin.readline())
dp = [0] * int(N+1)
for i in range(2,N+1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] =min(dp[i],dp[i//2]+1)
if i % 3 == 0:
dp[i] = min(dp[i],dp[i//3]+1)
sys.stdout.write(f"{dp[N]}\n")
가장 작은문제부터 시작하는 Bottom-up방식
dp[n] -> n을 1로 만들때 필요한 최소 연산횟수
dp = [0] * int(N+1) -> dp 공간 초기화
for i in range(2, N+1) -> dp[1]은 위에서 이미 0으로 초기화 했으니 dp[2]부터 dp[N]까지
dp[i] = dp[i-1] + 1 -> 1 더하는 연산을 기본으로 두고 i가 2로 나눠지면 dp[i]와 dp[i // 2]를 비교후 최솟값을 저장
dp[i]는 이전에 계산한 dp[i-1] + 1을 갖고오는것
dp[4] = min(dp[3] + 1, dp[2] + 1) = 2 ( 4 -> 2 -> 1)
dp[i // 2] + 1는 dp[i // 2]까지 필요한 최소 연산횟수에 + 1을 한것
3의 경우도 마찬가지
추가로 elif를 사용하지 않은 이유는 1까지 가는 최소 경로를 찾아야 하기 때문이다.
3으로 먼저 나누면 elif를 사용해도 되지않을까 했지만 아니였음 ㅎㅎ
구현은 쉬운데 구상이 어려우니 익숙할때까지 계속 풀어보자
'공부 > 코딩테스트' 카테고리의 다른 글
| [백준 2805번] | 나무 자르기 | 이분탐색, 이진탐색, Binary search (파이썬) (0) | 2025.02.15 |
|---|---|
| [백준 11659번] | 구간합, 누적합(prefix sum) | DP (파이썬) (0) | 2025.02.10 |
| [백준 1003번] | 피보나치 함수 | DP (파이썬) (0) | 2025.02.09 |
| 파이썬 빠른 입출력(readline, write) (0) | 2025.01.31 |
| Python EOF 해결 (0) | 2025.01.20 |





